Mac-forge experiment

$\text{Mac-forge}_{\mathcal{A},\Pi}(n)$:

1. A key k is generated by running $\text{Gen}(1^n)$.
2. The adversary $\mathcal{A}$ is given input $1^n$ and oracle access to $\text{Mac}_k(\cdot)$. The adversary eventually outputs $(m,t)$. Let $\mathcal{Q}$ denote the set of all queries queries that $\mathcal{A}$ asked its oracle.
3. $\mathcal{A}$ succeeds if and only if $\text{Vrfy}_k(m,t) = 1$ and $m \notin \mathcal{Q}$. In that case the output of the experiment is defined to be 1.

Definition 4.2

A message authentication code $\Pi = (\text{Gen},\text{Mac},\text{Vrfy})$ is existentially unforgeable under an adaptive chosen-message attack, or just secure, if for all probabilistic polynomial-time adversaries $\mathcal{A}$ there is a negligible function $\text{negl}$ such that:

Mac-sforge experiment

$\text{Mac-sforge}_{\mathcal{A},\Pi}(n)$:

1. A key k is generated by running $\text{Gen}(1^n)$.
2. The adversary $\mathcal{A}$ is given input $1^n$ and oracle access to $\text{Mac}_k(\cdot)$. The adversary eventually outputs $(m,t)$. Let $\mathcal{Q}$ denote the set of all queries that $\mathcal{A}$ asked its oracle, along with the response.
3. $\mathcal{A}$ succeeds if and only if $\text{Vrfy}_k(m,t) = 1$ and $(m,t) \notin \mathcal{Q}$. In that case the output of the experiment is defined to be 1.

Definition 4.3

A message authentication code $\Pi = (\text{Gen}, \text{Mac}, \text{Vrfy})$ is strongly secure, or a strong MAC, if for all probabilistic polynomial-time adversaries $\mathcal{A}$, there is a negligible function negl such that: here is a negligible function $\text{negl}$ such that: $Pr[\text{Mac-sforge}_{\mathcal{A},\Pi}(n)=1] \leq \text{negl}(n)$

Construction 4.5

Let F be a pseudorandom function. Define a fixed-length MAC for messages of length n as follows:

• $\text{Mac}$: on input a key $k \in \{0, 1\}^n$ and a message $m \in \{0, 1\}^n$, output the tag $t := \text{F}_k(m)$. (If $|m| = |k|$ then output nothing.)

• $\text{Vrfy}$: on input a key $k \in \{0, 1\}^n$, a message $m \in \{0, 1\}^n$, and a tag $t \in \{0, 1\}^n$, output 1 if and only if $t = \text{F}_k(m)$. (If $|m| = |k|$, then output 0.)

Theorem 4.6

If $\text{F}$ is a pseudorandom function, then Construction 4.5 is a secure fixed-length MAC for messages of length $n$.

or:

Proof

We use the proving strategy of analyzing the scheme using truly random functions, and then proving that the security loss incurred by using pseudo-random functions insead is negligible.

Let $\widetilde{\Pi}$ and $\Pi$ denote the scheme from construction 4.5, except that $\widetilde\Pi$ uses a truly random function $f$ instead of $\text{F}_k$

It follows that

Because $\widetilde\Pi$ directly applies $f$, and because for any message $m \not\in \mathcal{Q}$, the value $t = f(m)$ is uniformly distributed in ${0, 1}^n$ from the point of view of the adversary $\mathcal{A}$.

From

It follows that if

$|\text{Pr}[\text{Mac-forge}_{\mathcal{A},\Pi}(n) = 1]$ $-$ $\text{Pr}[\text{Mac-forge}_{\mathcal{A},\widetilde{\Pi}}(n) = 1]| \le negl(n)$ (4.2)

then

Proof by Distinguisher

1. Run $\mathcal{A}(1^n)$. Whenever $\mathcal{A}$ queries its MAC oracle on a message m (i.e., whenever $\mathcal{A}$ requests a tag on a message $m$), answer this query in the following way: Query $\mathcal{O}$ with m and obtain response t; return $t$ to $\mathcal{A}$.
2. When $\mathcal{A}$ outputs $(m, t)$ at the end of its execution, do:
   1. Query $\mathcal{O}$ with $m$ and obtain response $\tilde t$.
   2. If (1) $\tilde t = t$ and (2) $\mathcal{A}$ never queried its MAC oracle on $m$, then output 1; otherwise, output 0.

Proof by Distinguisher

Since the view of $\mathcal{A}$ inside $D$ is distributed identically to that of $\mathcal{A}$ in $\text{Mac-forge}_{\mathcal{A},\Pi}(n)$, and since $D = 1$ exactly when $\text{Mac-forge}_{\mathcal{A},\Pi}(n) = 1$:

and

and

Gives

Since $D$ runs in polynomial time.

Hence equaion (4.2) is proven!

Problem:

Construction 4.5 only works for small messages; same length as the key!

We can fix that. For a message $m_1,\ldots,m_d$ of $d$ $n$-length blocks, let

$$t_{1\ldots i \ldots d} = \text{Mac}_k(m_i)$$

Then use $t$ as the tag of $m$.

More Problems:

1. Re-ordering attack
   Solved by adding $i$ to $m_i$

2. Truncation attack
   Solved by adding message length $l$ to $m_i$

3. Mix ‘n’ match Solved by adding a random message id $r$ to $m_i$

We get:

$$t_{1\ldots i \ldots d} = \text{Mac}_k(r||l||i||m_i)$$

This is impractical. The message length is still fixed, and the message-space got a lot smaller.

Construction 4.11

Let $F$ be a pseudorandom function, and fix a length function $l > 0$. The basic CBC-MAC construction is as follows:

• $\text{Mac}$: on input of key $k \in \{0,1\}^n$ and a message $m$ of length $l(n)*n$, do the following (we set $l = l(n)$ in what follows):
  1. Parse $m$ as $m = m_1, ..., m_l$ where each $m_i$ is of length $n$.
  2. Set $t_1 := F_k(m_1)$. Then for $1 < i \leq l$:
     $\quad$ Set $t_i := F_k(m_i \oplus t_{i-1})$

  Output $t_l$ as the tag.

• $\text{Vrfy}$: on input a key $k \in \{0,1\}^n$, a message $m$, and a tag $d$, do: If $m$ is not length $l(n)*n$ then output $0$. Otherwise, output $1$ if and only if $t =^? \text{Mac}_k(m)$

(Length check + canonical verification.)

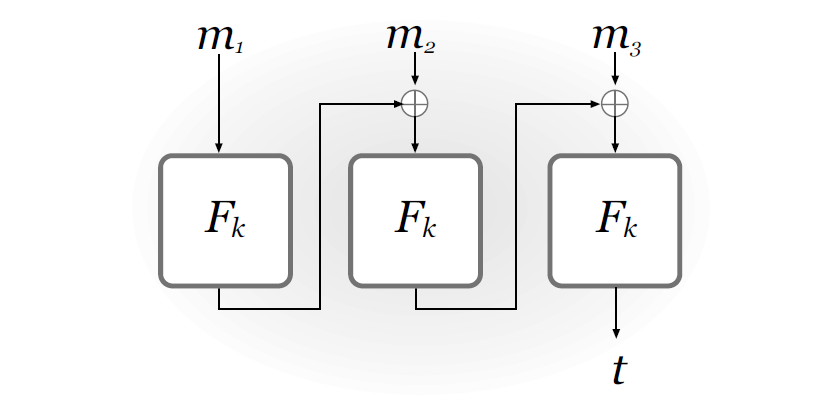
Is it ordering attack safe?

Is it truncation attack safe?

Is it mix ‘n’ match attack safe?

New problem: prefix attack

(This scales to arbitrary length messages.)

Prefix attack solution

Prefix the length:

$\text{Mac'}_k( \langle m_1, m_2 \rangle )$ $\neq \text{Mac'}_k( m_2 \oplus \text{Mac'}_k(m1) )$

$F_k(m_2 \oplus F_k(m_1 \oplus F_k(2)))$ $\neq F_k(m_2 \oplus F_k(m_1 \oplus F_k(1)) \oplus F_k(1))$

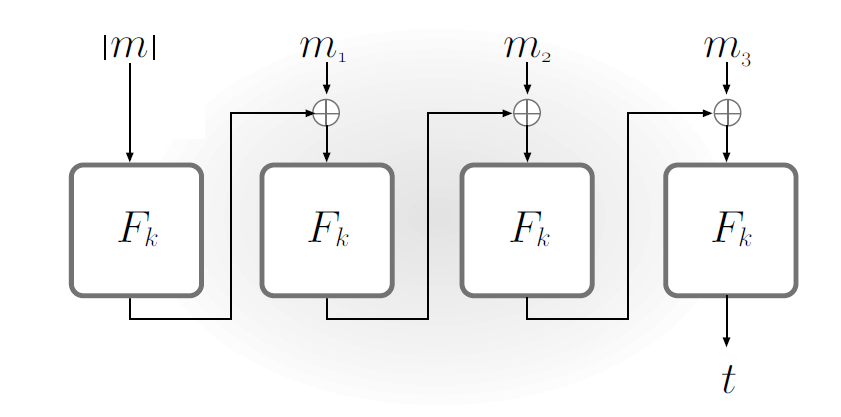
(hold on to your horses)

CBC-MAC

Proof of Security

“intended for advanced readers.”

$F$ is a keyed function that, for security parameter $n$, maps $n$-bit keys and $n$-bit inputs to $n$-bit outputs.

$\text{CBC}$ is a keyed function that, for security parameter $n$, maps $n$-bit keys and inputs in $(\{0,1\}^n)^*$ to $n$-bit outputs.

$\text{CBC}_k(x_1,...,x_l) \stackrel{\text{def}}{=}$ $F_k(F_k(\cdots F_k(x_1) \oplus \cdots ) \oplus x_l)$

Exactly like CBC-MAC, but without a fixed length-function ($l$ may vary).

A set of strings $P \subset (\{0,1\}^n)^*$ is prefix-free if it does not contain the empty string, and no string $X \in P$ is a prefix for any other string $X' \in P$.

Theorem 4.13

If $F$ is a pseudorandom function, then $\text{CBC}$ is a pseudorandom function on prefix-free inputs: for all probabilistic polynomial-time distinguishers $D$ that query their oracle on a prefix-free set of inputs, there is a negligible function $\text{negl}$ such that:

$| { \text{Pr}[D^{\text{CBC}_k(\cdot)}(1^n) = 1] - \text{Pr}[D^{f(\cdot)}(1^n) = 1] } |$ $\leq \text{negl}(n)$,

We can make $\text{CBC}_k$ work as a pseudorandom function for arbitrary-length inputs by converting these inputs to belong to the proper input space.

To get a tag from arbitrary length message $m$:

This is based on theorem 4.6, for secure fixed-length MACs. It works because $\text{encode}(m)$ ensures that the messages are unique.

How do we implement $\text{encode}$?

(a) Fix the length $l$, and then simply:
$\text{encode}(m) = m$

(b) Prepend the length:
$\text{encode} ( \langle m_1, ... m_{| m |} \rangle ) =$ $\langle n, m_1, ... m_{|m|-1}, \text{pad}(m_{|m|}) \rangle$

where $\text{pad}$ pads a message with 0s until it has the valid block length.

We want to prove that the security of $\text{CBC}$ depends solely on the security of $F_k$.

First, we replace $F_k$ in $\text{CBC}$ with a random function $g$ that maps $n$-bit inputs to $n$-bit outputs for security parameter $n$.

We need to show: if $g$ is chosen uniformly in $\text{Func}_n$, then $\text{CBC}_g$ is indistinguishable from a random function mapping $(\{0,1\}^n)^*$ to $n$-bit strings, as long as the set of inputs queried is prefix-free.

Claim 4.14

Fix any $n \geq 1$. For all distinguishers $D$ that query their oracle on a prefix-free set of $q$ inputs, where the longest input contains $l$ blocks, it holds that:

$| \text{Pr}[D^{\text{CBC}_g( \cdot )}(1^n) = 1] - \text{Pr}[D^{f(\cdot)}(1^n) = 1] |$ $\leq \frac{q^2 l^2}{2^n}$

where $g$ is chosen uniformly from $\text{Func}_n$, and $f$ is chosen uniformly from the set of functions mapping $(\{0,1\}^n)^*$ to $\{0,1\}^n$.

Notice that for any $t_1,...,t_q \in \{0,1\}^n$ it holds:

$\text{Pr}[ \forall i : f(X_i) = t_i ] = \frac{1}{2^{nq}}$

Proof of claims 4.14-15

First we show that $\text{CBC}$ is smooth. Then we show that smoothness implies claim 4.14.

Fix some $n \geq 1$.

Let $P \subset \{X_1,...X_q\}$ be a prefix-free set of inputs $X_i \in (\{0,1\}^n)^*$.

Let $l$ be the length (in blocks) of the longest input $X_i$.

We define smoothness:

$\text{CBC}$ is $(q,l,\delta)$-smooth if for every $P$ and every $t_1,...t_q \in \{0,1\}^n$, it holds that:

with the probability uniform over choice of $g \in \text{Func}_n$.

We will show that $\text{CBC}_g$ is $(q,l,\delta)$-smooth for $\delta = \frac{q^2 l^2}{2^n}$. (Claim 4.15)

$C_g(X) = (I_1, \dots, I_m)$ denotes the set of inputs on which $g$ is evaluated during the computation of $\text{CBC}_g(X)$ for any $X \in (\{0,1\}^n)^*)$ with $X = x_1, ...$ and $x_i \in \{0,1\}^n$.

Now let’s look at two different messages with a different number of blocks:

$X \in (\{0,1\}^n)^m \quad X' \in (\{0,1\}^n)^{m'}$

There is a non-trivial collision if for $i$ and $j$ it holds that $I_i = I_j$, but $i \neq j$.

There is a non-trivial collision in $X,X' \in P$ if for $i$ and $j$ it holds that $I_i = I'_j$, but $\langle x_1, ..., x_i \rangle \neq \langle x'_1, ..., x'_j \rangle$

Let $\text{Coll}$ be the event that such a collision occurs.

With no non-trivial collision:

We choose each output value for $g$ for a given input the first time it is requested. Each time, we choose it randomly. (Not efficient, but very uniformly chosen.)

Fun fact: We do not need to choose $g(I_m)$ and $g(I'_{m'})$ to determine if there is a collision: If the last elements collide it can only be because $X$ is a prefix of $X'$, but $P$ is prefix-free.

No non-trivial collision occurs.

All values fixed by $g$, including $\text{CBC}_g(X_1),...,\text{CBC}_g(X_q)$ are uniform and independent of each other.

This means that or any $t_1,...,t_q \in \{0,1\}^n$:

$\text{Pr}[ \forall i : \text{CBC}_g(X_i) = t_i | \overline{\text{Coll}} ] = \frac{1}{2^{nq}}$

Let us find an upper bound for $\text{Pr}[\text{Coll}]$:

$\text{Coll}_{i,j}$ is a collision between or within any fixed $X_i, X_j \in P$. So $\text{Coll}$ is the union of all $\text{Coll}_{i,j}$ for all $i, j$ within the length of $P$ (up to $q$). (All unique collisions between or within inputs.)

Using union-bound:

$= \begin{pmatrix}q\\2\end{pmatrix} * \text{Pr}[\text{Coll}_{i,j}] \leq \frac{q^2}{2} * \text{Pr}[\text{Coll}_{i,j}]$

Let us find upper bound for $\text{Pr}[\text{Coll}_{i,j}]$:

Probability of any collision is larger with longer inputs, so we fix two inputs $X, X'$ with length $l$ (max length).

Fix $t$ as the largest integer such that $(x_1,...,x_t) = (x'_1,...,x'_t)$.

1. For $i = 1,...,t-1$ fix $g(I_i)$ uniformly. (steps $1$ to $t-1$)
2. Fix $g(I_t)$ uniformly. (step $t$)
3. For $i = t+1,...,l-1$ choose $g(I_i)$ uniformly. (steps $t+1$ to $l-1$)
4. For $i = t+1,...,l-1$ choose $g(I'_i)$ uniformly. (steps $l$ to $2l-2$)

$\text{Coll}(k)$ is the event that a non-trivial collision occurs by step $k$.

$\text{Pr}[\text{Coll}_{i,j}]$ $= \text{Pr}[\bigtriangleup_k \text{Coll}(k)}]$ $\leq \text{Pr}[Coll(1)] + \stackrel{2l-2}{\sum_{k=2}} \text{Pr}[\text{Coll}(k)|\overline{\text{Coll}(k-1)}]$

Probability of collision first at step $k < t$ is $k/2^n$ (attempts over block space).

Probability of collision first at step $t$ is $leq 2t/2^n$ (2 values: 2 times attempts over block space).

Probability of collision first at step $k > t$ is $(k + 1)/2^n$. (attempts + 1 over block space) [why?]

$< \frac{2l^2}{2^n}$

Recall

$\text{Pr}[\text{Coll}] < \frac{q^2l^2}{2^n} = d$

Definitions

$\text{Enc-forge}_{\mathcal{A},\Pi}(n)$:

1. Run $\text{Gen(1^n)}$ to obtain a key $k$

2. The adversary $\mathcal{A}$ is given input $1^n$ and access to an encryption oracle $\text{Enc}_k(\cdot)$. The adversary outputs a ciphertext $c$.

3. Let $m := \text{Deck}(c)$, and let $\mathcal{Q}$ denote the set of all queries that $\mathcal{A}$ asked its encryption oracle. The output of the experiment is 1 if and only if (1) $m \ne \bot$ and (2) $m \not\in \mathcal{Q}$.

Definition 4.16

A private-key encryption scheme $\Pi$ is unforgeable if for all probabilistic polynomial-time adversaries $\mathcal{A}$, there is a negligible function $negl$ such that:

Definition 4.17

A private-key encryption scheme is an authenticated encryption scheme if it is CCA-secure and unforgeable.

This is the strongest security definition yet!

Generic constructions

Goal: Come up with a construction that combines any CPA-secure encryption scheme with any unforgeable $\text{Mac}$ to achieve authenticated encryption.

Given $Enc_{k_E}(x)$, $Mac_{k_M}(y)$, come up with ciphertext and tag $\langle c,t\rangle$.

Three obvious constructions:

1. Encrypt and authenticate
   $c\leftarrow Enc_{k_E}(m)$, $t\leftarrow Mac_{k_M}(m)$

2. Authenticate then encrypt
   $t\leftarrow Mac_{k_M}(m)$, $c\leftarrow Enc_{k_E}(m||t)$

3. Encrypt then authenticate
   $c\leftarrow Enc_{k_E}(m)$, $t\leftarrow Mac_{k_M}(c)$

1. Encrypt and authenticate

$c\leftarrow Enc_{k_E}(m)$, $t\leftarrow Mac_{k_M}(m)$

Nope.
Unforgabilty does not guarantee secrecy; $t$ may leak information about $m$

2. Authenticate then encrypt

$t\leftarrow Mac_{k_M}(m)$, $c\leftarrow Enc_{k_E}(m||t)$

Nope.
Mumble mumble, padding oracle attack, mumble mumble

3. Encrypt then authenticate

$c\leftarrow Enc_{k_E}(m)$, $t\leftarrow Mac_{k_M}(c)$

Yes!

Construction 4.18

Let $\Pi_E = (\text{Enc}, \text{Dec})$ be a private-key encryption scheme and let $\Pi_M= (\text{Mac}, \text{Vrfy})$ be a message authentication code, where in each case key generation is done by simply choosing a uniform $n$-bit key. Define a private-key encryption scheme $(\text{Gen}', \text{Enc}', \text{Dec}')$ as follows:

Construction 4.18

• $\text{Gen}'$: on input $1^n$, choose independent, uniform $k_E, k_M \in {0, 1}^n$ and output the key $(k_E, k_M)$.

• $\text{Enc}'$: on input a key $(k_E, k_M)$ and a plaintext message $m$, compute $c \leftarrow \text{Enc}_{k_E}(m)$ and $t \leftarrow \text{Mac}_{k_M}(c)$. Output the ciphertext $\langle c, t\rangle$.

• $\text{Dec}'$: on input a key $(k_E, k_M)$ and a ciphertext $\langle c, t\rangle$, first check whether $\text{Vrfy}_{k_M}(c, t) = 1$. If yes, then output $\text{Dec}_{k_E}(c)$; if no, then output $\bot$.

Intution:

1. Since $\text{Mac}$‘ing is the final step, unforgeability is implied!
2. Since an adversary cannot hope to forge a valid ciphertext, the CCA decryption oracle is useless; CPA implies CCA!

Theorem 4.19

Let $\Pi_E$ be a CPA-secure private-key encryption scheme, and let $\Pi_M$ be a strongly secure message authentication code. Then Construction 4.18 is an authenticated encryption scheme.

Strategy:

Show that strong security of $\Pi_M$ implies that any “new” ciphertexts submitted by $\mathcal{A}$ will be invalid.

Definitions:

• a ciphertext $\langle c,t\rangle$ is $new$, if $\mathcal{A}$ did not receive it from the encryption oracle
• $\text{ValidQuery}$ is the event that $\mathcal{A}$ submits a $new$, valid, $\langle c,t \rangle$ to the decryption oracle.

Claim 4.20

$\text{Pr}[\text{ValidQuery}]$ is negligible

Proof of 4.20

Intuitively (again): If $\mathcal{A}$ can forge a valid ciphertext, it has beaten $\text{Mac-sforge}$

Proof of 4.20

Formally: We construct an adversary $\mathcal{A}_M$ attacking $\Pi_M$ by running a a $\text{Mac-sforge}$ adversary $\mathcal{A}$.

Let $q(\cdots)$ be a polynomial upper-bound on the number of decryption-oracle queries made by $\mathcal{A}$

1. Choose uniform $k_E \in \{0, 1\}^n$ and $i \in \{1, . . ., q(n)\}$.
2. Run $\mathcal{A}$ on input $1^n$. When $\mathcal{A}$ makes an encryption-oracle query for the message $m$, answer it as follows:
   1. Compute c ← EnckE(m).
   2. Query $c$ to the MAC oracle and receive $t$ in response. Return $\langle c,t\rangle$ to $\mathcal{A}$.

The challenge ciphertext is prepared in the exact same way (with a uniform bit $b \in \{0, 1\}$ chosen to select the message mbthat gets encrypted).

When $\mathcal{A}$ makes a decryption-oracle query for the ciphertext $\langle c,t \rangle$ answer it as follows: If this is the ith decryption-oracle query, output (c, t).j0 Otherwise:

1. If $\langle c, t \rangle$ was a response to a previous encryption-oracle query for a message m, return m.
2. Otherwise, return ⊥.